por Anthony Carpi, Ph.D., Anne E. Egger, Ph.D.
DATOS CLAVES
- La incertidumbre es una estimación cuantitativa del error que está presente en todos los datos; todas las medidas contienen alguna incertidumbre generada a través del error sistemático y o del error común.
- Reconocer la incertidumbre de los datos es un componente importante en la presentación de los resultados de la investigación científica.
- La incertidumbre es malentendida comúnmente como que significa que los científicos no están seguros de sus resultados, pero el término especifica el grado por el cual los científicos sí están seguros de sus datos.
- La cuidadosa metodología puede reducir la incertidumbre al correr el error sistemático y minimizar el error aleatorio. Sin embargo, la incertidumbre nunca puede ser reducida a cero.
La incertidumbre y el error en la práctica – la datación por carbono 14
Los arqueólogos, paleontólogos y otros investigadores se han interesado durante mucho tiempo en la datación de objetos y artefactos, en un esfuerzo de comprender su historia y sus usos. Desafortunadamente, los registros escritos son una invención humana relativamente reciente y hay pocos artefactos históricos acompañados de historias escritas precisas. En la primera mitad del siglo XX, un químico nuclear americano llamado Willard F. Libby, se interesó en el uso del
isótopo radioactivo
14C para datar ciertos objetos. La
teoría de la datación por radiocarbono es relativamente sencilla. La mayoría del carbono en la estratosfera de la Tierra está como
12C, pero una pequeña cantidad del isótopo
14C, está producido naturalmente a través del bombardeo del
14N con rayos cósmicos (
W. F. Libby, 1946). A medida que las plantas captan carbono de la atmósfera a través de la respiración, incorporan el
14C, así como el más abundante
12C en sus tejidos. Los animales también toman los isótopos de carbono a través de la comida que comen. Por consiguiente, todos los
organismos vivos tienen la misma proporción de isótopos de
14C y
12C en sus cuerpos, que los que tiene la atmósfera. Al contrario del
12C, el
14C es un isótopo radioactivo que en su
producto 14N está constantemente sufriendo descomposición a un índice conocido. Mientras que un organismo está vivo, toma nuevo
14C del ambiente y así se mantiene en equilibrio con éste. Cuando los organismos mueren, sin embargo, el carbono en sus tejidos ya no se sustituye, y la cantidad de
14C disminuye lentamente con el tiempo al descomponerse en
14N. Por consiguiente, la cantidad del
14C radioactivo que se conserva en un pedazo de madera o hueso animal puede ser usado para determinar cuándo murió ese organismo. Esencialmente, a mayor tiempo de muerte del organismo, menores niveles de
14C.
La cantidad de material radioactivo (como el
14C) en un ejemplar, puede ser cuantificada al contar la cantidad de descomposición que sufre el material en un tiempo específico, usualmente presentados en cuentas por minuto (cpm). Cuando Libby empezó su
trabajo sobre el radiocarbono, en los años 1940, la tecnología disponible todavía era muy reciente. El sencillo contador Geiger se inventó recién en 1908 por el científico alemán Hans Wilhelm Geiger, un estudiante de Ernest Rutherford, y no fue perfeccionado hasta 1928, cuando Walther Müller, un alumno de Geiger, mejoró el diseño permitiendo la detección de todos los tipos de radiación. Se le atribuye al mismo Libby la construcción del primer contador Geiger en los Estados Unidos en los años 1930. Pero se enfrentó a un gran obstáculo al usar el instrumento para medir la radiación del
isótopo 14C de los rayos cósmicos de fondo y de la Tierra que ocurren naturalmente, y la variabilidad asociada con la señal de fondo que podía inundar la pequeña señal del
14C que él esperaba detectar. En 1949, Libby informó sobre un método para deducir la señal de fondo y la variabilidad. Puso el ejemplar entero y el detector dentro de un tubo cubierto de 2 pulgadas de plomo y 4 pulgadas de hierro (
W. F. Libby, Anderson, & Arnold, 1949). De esta manera, Libby y sus colegas redujeron la señal de fondo de 150 cpm a 10 cpm y minimizaron la variabilidad asociada a la señal a “alrededor de 5-10% de error”, o menos de 1 cpm. Libby y sus colegas no usan la palabra error como lo hacemos en el lenguaje común, donde se refiere a un error como el error tipográfico o de baseball. El origen latino de la palabra error (
errorem) significa
deambular o
perdido, y el uso científico de la palabra está más cercano a su significado original. Libby calculó el error asociado a sus medidas al contar la cantidad de eventos de descomposición en el ejemplo, durante una cantidad de tiempo conocida, repitiendo las medidas durante múltiples periodos y usando técnicas estadísticas para cuantificar el error, después (vea nuestro módulo
Data: Statistics).
En 1949, Libby, trabajando con su estudiante posdoctoral James Arnold, presentó el primer uso de la datación de radiocarbono para determinar la edad de los fragmentos de madera de sitios arqueológicos alrededor del mundo (
Arnold & Libby, 1949). Debido a que el método era nuevo, Arnold y Libby tuvieron cuidado en replicar sus medidas para proveer un estimado detallado de diferentes tipos de error, y compararon los resultados de sus métodos con los ejemplares de una edad conocida como el control (Tabla 1).
Table 1. Las determinaciones de la edad en ejemplares de edad conocidas de Arnold y Libby (
1949).
| Sample | Specific activity (cpm/g of carbon) | Age (years) |
| Found | Found | Expected |
| Tree Ring | 11.10 ± 0.31 | 1100 ± 150 | 1372 ± 50 |
| | 11.52 ± 0.35 | | |
| | 11.34 ± 0.25 | | |
| | 10.15 ± 0.44 | | |
| | 11.08 ± 0.31 | | |
| | Average : 10.99 ± 0.15 | | |
En la tabla 1 se ven las actividades especificas para cinco duplicados diferentes de un ejemplar de madera de un abeto Douglas, excavado en el Valle Red Rock. Cada medida individual tiene un error a su derecha, indicado con el signo ±. Arnold y Libby describen estas medidas en su
trabajo, planteando que “Los errores citados para una medida de una actividad específica son desviaciones estándares computadas de las estadísticas Poisson del conteo de eventos aleatorios.” En otras palabras, el error individual está calculado sobre la
base de incertidumbres esperadas, asociadas a la descomposición radioactiva para cada ejemplar. Tal como se ve en la Tabla 1, en la
parte inferior se provee un error general de un valor promedio de una actividad específica (10.99). El error general (0.15) es menor al error individual presentado con cada medida. Esta es una importante característica del cálculo estadístico del error asociado con los
datos científicos – a medida que aumentamos el número de medidas para un valor, disminuye la incertidumbre y aumenta la seguridad asociada con la aproximación del valor. El error presentado junto a la actividad específica provee una medida de la
precisión del valor y es referido comúnmente como un
error estadístico. El error estadístico es lo que Pearson describe como la incertidumbre inherente de la medida. Está causada por las fluctuaciones aleatorias de la descomposición radioactiva y a veces se lo conoce como error aleatorio, ya que el investigador tiene poco control sobre el mismo. El error estadístico no puede ser eliminado, como describió Pearson, pero
si puede ser medido y reducido cuando se hacen repetidas observaciones de un evento específico.
En la columna 3 de la tabla 1, Arnold y Libby estiman la edad del ejemplar del abeto Douglas, basándose en la actividad del
14C como de 1100 años (datando su primera temporada de crecimiento en el año 849 de nuestra era). En la columna 4 de tabla 1, informan de la edad real del abeto Douglas, calculada al contar los tres anillos en el ejemplar como de 1372 años (datando su primera temporada en el año 577 de nuestra era). Al comparar la edad del
14C al valor teóricamente correcto determinado al contar los tres anillos, Arnold y Libby le permiten al lector evaluar la
exactitud de su método, y esto provee la medida de un segundo tipo de error que se encuentra en la ciencia: el
error sistemático. Basándose en sus
datos, Arnold y Libby plantean que el “acuerdo entre la predicción y la observación parece ser satisfactorio.” Sin embargo, a medida que Libby continuó investigando para establecer el método de la datación por
14C, Libby empezó a reconocer que la discrepancia entre la datación del radiocarbono y otros métodos era aún mayor para los objetos más antiguos, especialmente aquellos de más de 4000 años (
W.F. Libby, 1963). Mientras que las fechas teóricamente correctas en los objetos muy antiguos pueden establecerse por otros medios, como en los ejemplares de los templos de Egipto donde existía un
sistema de calendario bien establecido, las edades obtenidas a través de la datación por radiocarbono eran constantemente mayores a las fechas registradas, frecuentemente, tanto como 500 años. Libby sabía que habría errores estadísticos en estas medidas y había anticipado el uso de la datación por
14C para calcular una gama de fechas para los objetos. Pero el problema que encontró fue diferente: la datación por
14C calculaba sistemáticamente las edades que diferían tanto como 500 años de las edades reales de los objetos más antiguos. El error sistemático, como Libby encontró, se debía a una fluctuación desconocida pero no aleatoria, como el sesgo instrumental o una presunción fallida. El método de datación por radiocarbono ha logrado una buena
precisión. Los análisis duplicados produjeron fechas separadas entre sí por 150 años, como se puede ver en la Tabla 1; pero inicialmente demostró una precisión mala – la fecha del abeto de Douglas por
14C era casi 300 años diferente que la edad real, y otros objetos estaban errados como por 500 años.
Al contrario del
error estadístico, el
error sistemático puede ser compensado, o algunas veces eliminado,
si su fuente puede ser identificada. En el caso de la datación por
14C, se descubrió con posterioridad que la razón del error sistemático era una asunción fallida: Libby y muchos otros científicos habían asumido que el índice de producción del
14C en la atmósfera se mantenía constante en el tiempo, pero no es así. Al contrario, fluctúa con los cambios en el campo magnético terrestre, la toma de carbón por las plantas y otros factores. Adicionalmente, los niveles radioactivos de
14C aumentaron a lo largo del siglo XX, debido a que el ensayo de las armas nucleares despidió altos niveles de radiación a la atmósfera.
 |
©Hannes Grobe |
|
|
Figura 3: Se han usado las fechas provenientes de los anillos de los árboles para recalibrar el método de datación por radiocarbono. |
Desde que Libby publicó su método, los investigadores han recalibrado el método de datación por radiocarbono con la datación por los anillos de los árboles de pinos (
Damon et al., 1974) y de corales (
Fairbanks et al., 2005) para corregir las fluctuaciones en la producción de
14C en la atmósfera. Como consecuencia, la
precisión y la
exactitud de las fechas de radiocarbono han aumentado drásticamente. Por ejemplo, en el año 2000, Xiaohong Wung y sus colegas de la Universidad de Pekín en Beijing, usaron la datación por radiocarbono en los huesos de los marqueses de Jin rescatados de un cementerio en la provincia Shanxi en China (vea la Tabla 2) (
Wu et al., 2000). Tal como se puede ver en la Tabla 2, no sólo la precisión de los estimados (que van de los 18 a los 44 años) es más justa que la gama de error de 150 años que Libby presentó sobre los ejemplares de abetos de Douglas, sino que las fechas de radiocarbono concuerdan precisamente con las fechas reportadas de la muerte de Jin (los valores teóricamente correctos) que están dentro de la gama del
error estadístico en los tres casos.
Tabla 2. Los estimados de radiocarbono y las fechas documentadas de la muerte de tres de los marqueses de Jin, por Wu et al. (
2000).
Name of Jin Marquis | Radiocarbon Date (BCE) | Documented Death Date (BCE) |
| Jing | 860-816 | 841 |
| Li | 834-804 | 823 |
| Xian | 814-796 | 812 |
La confiabilidad: la presentación de la incertidumbre y el error
Como consecuencia del error, las medidas científicas no se reportan como valores sencillos, sino como gamas o promedios con barras de errores en un gráfico o signos de ± en una tabla. Karl Pearson primero describió los métodos matemáticos para determinar la distribución de la
probabilidad de las medidas científicas, y estos métodos forman la
base de las aplicaciones estadísticas en la investigación científica (vea nuestro módulo
Data: Statistics). Las técnicas estadísticas nos permiten estimar y reportar el error que rodea un valor, después de que se han repetido las medidas de ese valor. Por ejemplo, Libby y Wu reportaron sus estimados como registros de una
desviación estándar, alrededor de la medida
media, o promedio. La desviación estándar provee una medida del registro de variabilidad de medidas individuales y específicamente, define un registro que contiene un 34.1% de las medidas individuales por encima del valor medio y 34.1% de aquellos por debajo de la media. La desviación estándar de un registro de medidas puede ser usada para calcular un intervalo de confiabilidad alrededor del valor. Las declaraciones de confiabilidad no proveen, como creen algunos, un cálculo de cuán correcta es una medida. Por el contrario, una declaración de confiabilidad describe la probabilidad por la cual un registro de medidas se superpondrá al valor medio de la medida cuando se repite un estudio. Esto puede sonar un poco confuso, pero considere un estudio de Yoshikata Morimoto y sus colegas, quienes examinaron el promedio de la velocidad del lanzamiento de ocho jugadores de baseball de la universidad (
Morimoto et al., 2003). Cada uno de los pitchers tenía que hacer seis lanzamientos y el promedio de la velocidad fue de 34.6 m/s (77.4 mph) con un 95% de intervalo de confianza de 34.6 ± 0.2 m/s (34.4 m/s a 34.8 m/s). Más adelante, cuando repitió este estudio y cada uno de los 8 pitchers tenía que hacer 18 lanzamientos, el promedio de la velocidad fue de 34.7 m/s, exactamente dentro del intervalo de confianza obtenido durante el primer estudio. En este caso, no hay un valor “teóricamente correcto”, sino que el intervalo de confianza provee un estimado de la probabilidad de que se encontrará un resultado similar
si se repite el estudio. Debido a que Morimoto determinó un intervalo de confianza de 95%, si repitiese su estudio 100 veces (sin agotar a sus pitchers), su intervalo de confianza se superpondría con la media de la velocidad del lanzamiento 95 veces, y los otros cinco estudios probablemente, producirían velocidades de lanzamiento que estarían fuera del intervalo de confianza.
En la ciencia, un indicador importante de la confiabilidad para la medida es la cantidad reportada de cifras significativas. Morimoto reportó sus medidas a una décima (34.6 m/s) ya que su instrumentación tenía este nivel de
precisión. Pudo distinguir las diferencias en los lanzamientos de 34.6 m/s a 34.7 m/s.
Si hubiese redondeado sus medidas a 35 m/s, hubiese perdido una cantidad de detalles contenidos en sus
datos. Es más, su instrumentación no tenía la precisión necesaria para reportar figuras significativas adicionales (por ejemplo, 34.62 m/s).Cuando se reportan figuras significativas, se puede introducir errores substanciales en un conjunto de datos.
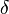 es su elongación o variación que experimenta su longitud.
es su elongación o variación que experimenta su longitud.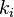 o
o  intrínseca, se tiene:
intrínseca, se tiene: a la tensión en una sección del muelle situada una distancia x de uno de sus extremos que tomamos como origen de coordenadas, kΔx a la constante de un pequeño trozo de muelle de longitud Δx a la misma distancia y δΔx al alargamiento de ese pequeño trozo en virtud de la aplicación de la fuerza F(x). Por la ley del muelle completo:
a la tensión en una sección del muelle situada una distancia x de uno de sus extremos que tomamos como origen de coordenadas, kΔx a la constante de un pequeño trozo de muelle de longitud Δx a la misma distancia y δΔx al alargamiento de ese pequeño trozo en virtud de la aplicación de la fuerza F(x). Por la ley del muelle completo: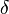 es su elongación o variación que experimenta su longitud.
es su elongación o variación que experimenta su longitud.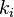 o
o  intrínseca, se tiene:
intrínseca, se tiene: a la tensión en una sección del muelle situada una distancia x de uno de sus extremos que tomamos como origen de coordenadas, kΔx a la constante de un pequeño trozo de muelle de longitud Δx a la misma distancia y δΔx al alargamiento de ese pequeño trozo en virtud de la aplicación de la fuerza F(x). Por la ley del muelle completo:
a la tensión en una sección del muelle situada una distancia x de uno de sus extremos que tomamos como origen de coordenadas, kΔx a la constante de un pequeño trozo de muelle de longitud Δx a la misma distancia y δΔx al alargamiento de ese pequeño trozo en virtud de la aplicación de la fuerza F(x). Por la ley del muelle completo: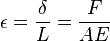











![\includegraphics[angle=0, width=0.8\textwidth]{fig03-07.eps}](http://www.bioestadistica.uma.es/libro/img494.gif)
![\includegraphics[angle=0, width=1\textwidth]{fig03-08.eps}](http://www.bioestadistica.uma.es/libro/img500.gif)

 enlarge image
enlarge image URANIA CECILIA MOLINA
URANIA CECILIA MOLINA